どうも、さわざわです。
今回は一風変わったシリーズとして、永田カレントミラーについて触れていこうと思うよ。回路としてはへぇーと思わせるような面白い回路だけど、アナログ回路の考え方としてもよく考えさせられる回路なので、頭の体操と思ってみんなも勉強していってねい。
この記事を読めば、永田カレントミラーについて小信号等価回路の観点から効能を理解できます。
永田カレントミラーの回路図
これは永田さんによって発明された回路だと思うんだけど、以下のような回路図になっているよ。
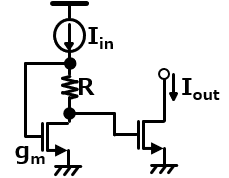
ポイントとしては通常のカレントミラーのように入力がダイオード接続になっているんだけど、間に抵抗Rが挟まっていることだね。入力のnchはダイオード接続なのでgm分の負荷が見えるね。
ここで線形抵抗であるRは固有の値にできてるとして、nchのgmは入力電流に依存して変動することになるよね。
もしここで、R=1/gmとなるように電流を設定したら、このカレントミラーはどのように働くだろう?一度考えてみてね。
次項で小信号等価回路として考えてみよう。
カレントミラーの記事は以下にまとめてあるので覗いてみてねん。
→カレントミラーについて
カスコードカレントミラーについて
低電圧カスコードカレントミラーについて
小信号等価回路からゲインを考えよう
ここではさっきの回路を以下のように切り出して、入力をvinとしてvoutへのゲインがどうなるかを考えていこう。
この場合に、voutまでの伝達経路が二つあるよね。なのでそれぞれの経路で伝達ゲインを独立に考えて、それを最後に足し合わせて考える重ね合わせの理で解いていこう。
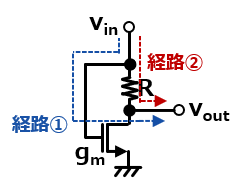
まずはnchにvinが入ってて、Rの上側はac0Vとして考えよう。そしたらこれってただのソース接地回路に見えてくるよね。なので伝達ゲインは簡単で、以下のように出せるね。
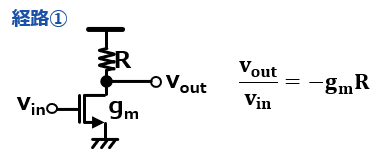
ソース接地回路は以下にまとめてあるよ。
→ソース接地回路について_小信号等価回路を理解しよう編
ソース接地回路について_小信号等価回路で伝達関数と周波数応答を出そう編
ソース接地回路について_いろいろなソース接地回路に触れよう編
次にnchの入力にはdc電圧のみ与えられてるとして、Rの上側にvinが入ってるとしよう。これって伝達ゲインがどうなるかな?
定電流源はRよりはるかに大きな抵抗として扱えるので、以下のような抵抗分圧にてゲインは1として出せるね。
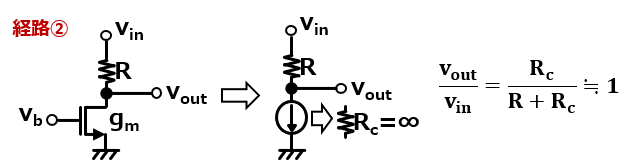
ここで言えるのは、こっちの経路に関しては飽和で駆動できているうちはgmやRはほぼ関係なくゲイン1になってるってことだね。
なので最終的なゲインは上記二つのパターンを足し合わせて以下のようになるね。
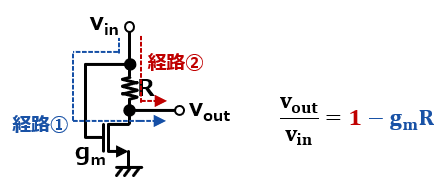
永田カレントミラーの効能
ここでカレントミラーに戻ると、gmは入力電流に依存して変動するパラメータなので、もし入力電流が小さくgmが小さくなり、1/gm>Rならさっきのゲインは+の値を持つことになるね。
一方で電流が大きく1/gm<Rならばゲインは-の値になるね。
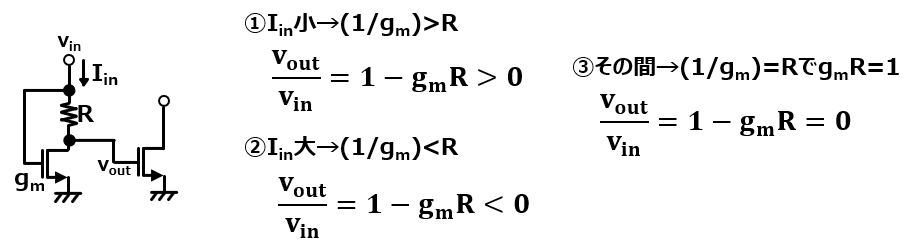
そしてその間の1/gm=Rのときには、gmR=1となることから伝達ゲインが0となるんだね。ゲインが0ってのは入力に対して出力が完全に寝て、入力からの感度が全くないことを指してるね。
ここでvinとIinは比例してるとして、voutも出力側のnchに入るだけなのでIoutと比例の関係で、IinとIoutの関係が以下のようになるよ。
ここでR=1/gmの領域ではIoutはIinの感度を持っていないことがわかり、その領域より小さいと正のゲイン、大きいと負のゲインを持っていることが確認できるね。
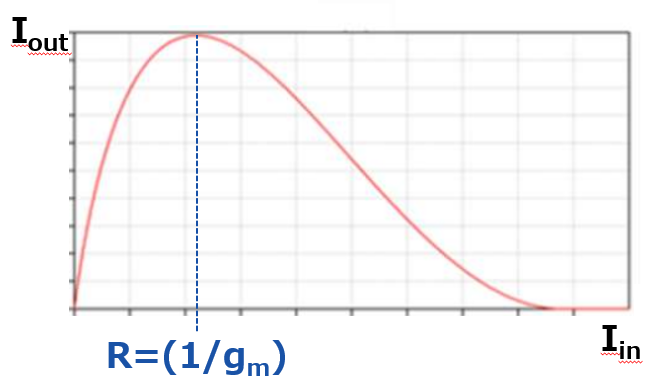
入力の感度を持たないってことは、dc的な電流は実現できている一方で、ノイズのようなac成分が入力に入っても伝達されないんだ。これによりノイズに強いカレントミラーを実現できることになるってわけだね。
アンプとかだけを考えてるとゲイン0ってよくわからないけど、こういった効能もあって面白いなって感じだね。
このカレントミラーについては以下にかかれているので読んでみてねん(中古だと安く手に入るイメージ)。他のアナログ回路についても丁寧に書かれているので持ってて損はない気がする。

今日はここまで、ほな。
雑談枠
ピザのハーフ&ハーフみたいなのをハンバーガーでもできんかなって思ったけど、ほぼmixされた味になるんかね。最近ハンバーガーが重いと思い始める者、ありけり。
おすすめ書籍紹介(Amazonに飛びます)

アナログCMOS集積回路の設計 (基礎編)
(最近第2版が出て原版のupdateが反映された感じ)

アナログCMOS集積回路の設計 (応用編)
(最近第2版が出て原版のupdateが反映された感じ、以下のソフトカバーと比較すると高い気が。。)

Design Of Analog Cmos Integrated Circuit , 2Nd Edition
(↑の原版のIndian版(英語)で2ndからは訳書にない新内容有り、ペーパーバックは安め。英語に抵抗ない方はこっち買うほうが内容的にも値段的にもお得)

Analog Integrated Circuit Design
(網羅的かつ設計観点で深めに学べる印象なのにわかりやすく書いてて初級向け、演習も易しめで取っつきやすい。ただハードカバーのため高い、、)

CMOSアナログ回路入門: LSI設計者のための (半導体シリーズ)
(初学者向け。実用的な内容もあるがあまり深ぼらないので、あくまで勉強するきっかけを作る本な気が。)
Xアカウント
https://x.com/swzw6112
–お問い合わせ–
以下よりお願いします。