どうも、さわざわです。
今回はSファクタとFDSOIについて触れていこうと思うよ。前回短チャネル効果とその対策について触れたけど、他の対策としてFDSOIのようなデバイス構造によるアプローチもあるよ。特に近年はMOSの形がどんどん変わっていって、デバイス構造による特性改善は競争の渦中にあるよ。今日はデバイスの内容になるけど、FDSOIにすることで従来のバルクMOSよりどんないいことがあるかをピックしていくよ。みんなも勉強していってねい。
前回の短チャネル効果の内容は以下だよ。
→微細化の凄みと短チャネル効果について
この記事を読めばFDSOIについて、従来のバルクMOSに対する利点をSファクタを含めて理解できます。
FDSOIって？不純物濃度を増やさずに済む！
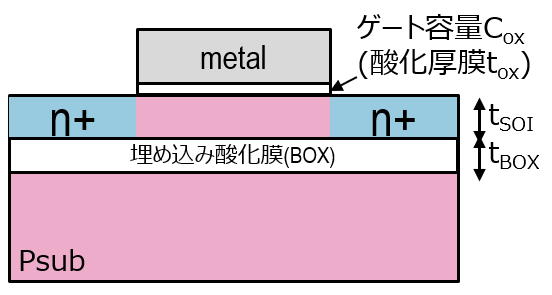
FDSOIは以下のようなでチャネルの下に埋め込みの酸化膜を挟んだプレーナー構造のMOSになっていて、FDってのは完全空乏って意味で空乏層の最大幅Wdmaxがtsoiより厚いとき、オン時にtsoi部分のSiが全て空乏層で埋まることからそう呼ばれているよ。
ちなみにWdmax<tsoiの場合PDSOI(部分空乏)って名前も特性も若干異なるけど今回は割愛するよ。
こういった構造で何がいいかだけど、まず前回短チャネル効果で出てきたパンチスルーを抑えられるよね。当然酸化膜には空乏層が伸びないから、チャネル下で空乏層が形成されることがなくなり、リーク経路を減らせるんだね。
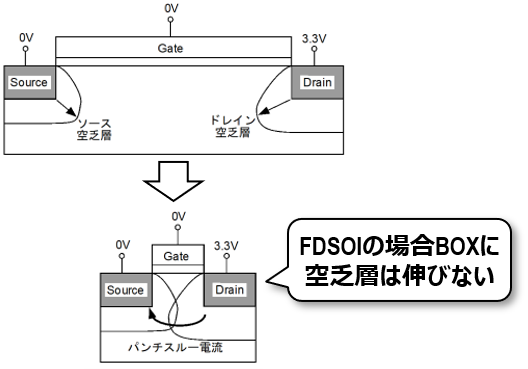
これはチャネル部の不純物濃度を増やしすぎずに済むんだね。これって前回挙げた短チャネル効果はいずれも、対策は結局はドーピング濃度を上げるってもんだったけど、前回言ったVth上昇しすぎるってもの以外にも、デメリットが多いんだね。
例えば不純物濃度が高いと、そのSi内を電荷が通る際に不純物がたくさんあって邪魔だよーってイメージなのかな、不純物散乱といって移動度の低下につながってしまうんだね。
あとは同じゲート面積でも不純物が大きくなるほどVthのばらつきも大きくなることが挙げられるよ。基本的には以下のようにVthのばらつきは不純物濃度の平方根に比例するよ。
最後は次項以降に説明するけど不純物濃度を上げるとSファクタが悪化していくんだね。SファクタをよくするにはこのFDSOIの構造が重要ってことで、話していくよ。
Sファクタって？
短チャネル効果って総じて、チャネルに形成される電荷の、ゲート電圧依存性が弱まるって現象なんだよね。リークだったりゲート電圧に依存しないVth変動だったり。
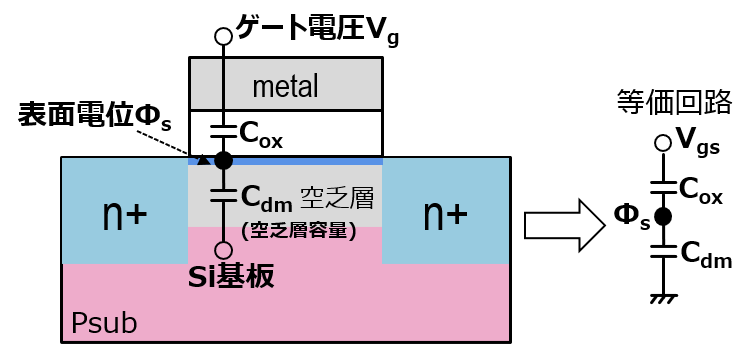
そこでゲート電圧によるスイッチング特性を表す指標として、Sファクタ(SS)というのがあって、以下のように表せるよ。ここでの2.3ってのは、ln10を表してるよ。
ここでCoxは酸化膜容量、Cdmはチャネル空乏層容量を表しているよ。意味としては電流を10倍するのに必要なVgsがいくらかってこと。できるだけ必要なVgsが小さいほうがいいわけだから、このSファクタは小さいほどスイッチングが急峻で、良い特性ということになるよ。
アナログ回路のgmに似てるけど、Sファクタはあくまでスイッチング特性(電流オフ→オン)を見ていることに注意だよ。
そしてSファクタの括弧の中だけど、これは以下のようにVgsに対する表面電位Φsの感度を表しているよ。要はVgsに対してΦsが変動しなかったら括弧の中は大きくなっていって、電流を増やすのにVgsをたくさんかけないといけないことになるよ。
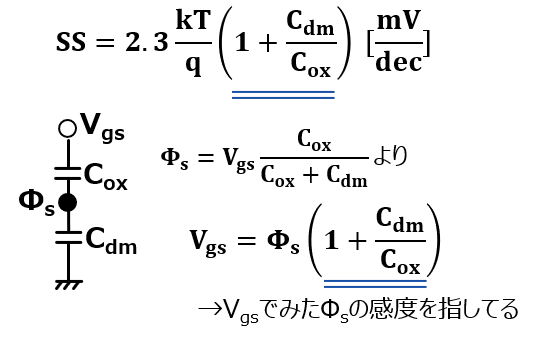
ここで重要なのはSファクタって室温において、下限があるってことだね。括弧の外は温度が室温なら定数になるので、仮にCoxに対してCdmがほぼ見えず、Vgsに対してΦsがほぼ追従したとしても、括弧の中は1になってSS=60mV/decとなるね。
これ以上SSを下げられないことが、スケーリング則にのっとらないパラメータとして微細化を苦しめていることも事実だよ。
FDSOIのSファクタにおける優位性を考察
じゃあここで、バルクMOSとFDSOIでSファクタの比較をしてみよう。バルクMOSの場合、以下のようにゲート酸化膜toxを1.1nmとしよう。んで、チャネル不純物濃度NA=2×1016cm-3だった場合に、Sファクタを上記の式に当てはめて計算するといくらになるだろう？
これには酸化膜容量Coxと空乏層容量Cdmを計算すればよいわけで、Coxは誘電率から以下のように計算できるね。ここでの材料はSiO2であるから、εox=3.9を用いていることに注意だよ。
次にCdmはNAから計算できるけど、フェルミエネルギーΦF→空乏層最大幅Wdmax→Cdmの順番で計算できるよ。
まずΦFは以下のように、
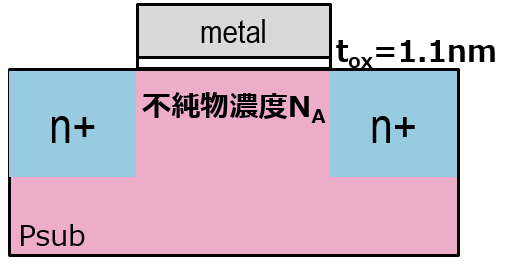
と計算できるね。特に注記はいれないけど、T=300Kで計算しとくよ。 次にWdmaxを計算すると、
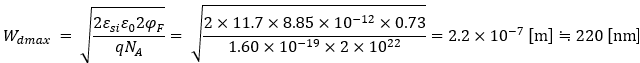
となるね。ここでNAは最初はm-3単位で計算してるよ。
あとはCoxと同様にCdmを計算すれば良くて、今回はチャネルで形成される容量として見れるわけだから、εSi=11.7を用いて以下のようになるよ。
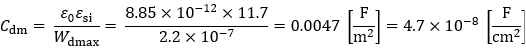
これでCoxとCdmを計算できたからSSの式に代入して値を見てみよう！
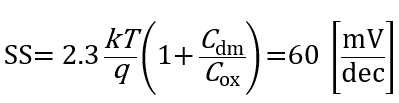
この結果から、Coxに対してCdmがほぼ見えないことから、SSは最小の値になっていることがわかるね。理想的にはこれでいいんだけど、前回説明した短チャネル効果が表れはじめるとリークが増えてきて、実際的にはSファクタは増加していってしまうんだね。
ここでは机上計算しかできないけど、短チャネル効果を防ぐためにNAを上げていくとどうなるか見ていこう。例えば100倍のNA=2×1018cm-3として同様にSファクタを計算してみよう。
まずCoxはNAに依らないからさっきと同じ値が入るね。Cdmが以下のように計算できるね。NAが大きくなったことでWdmaxが減っていることがうかがえるね。
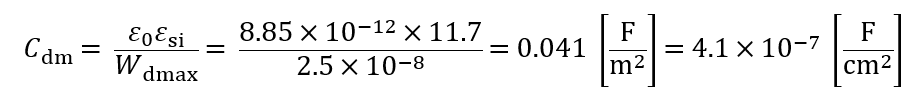
するとSファクタは以下のようになっていくね。
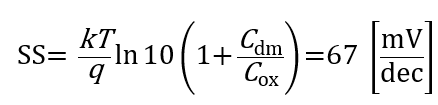
NA=2×1016cm-3→2×1018cm-3のSSの推移は以下のようになっているね。
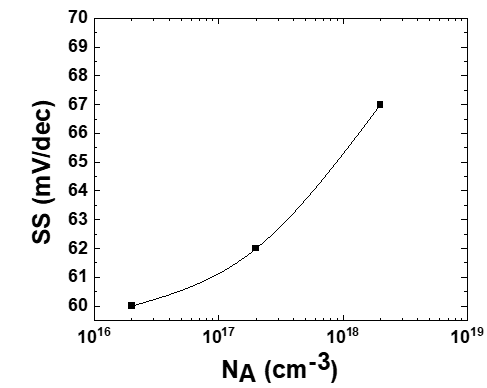
これは単純にNAを上げていくとCoxは変わらないのにCdmは大きくなっていくから徐々に無視できなくなって、SSがあがっていってしまうんだね。
では以上のことをFDSOIで計算してみようか。パラメータは以下のように、tox=1.1nm、tSOI=10nm、tBOX=100nmとしているよ。ここで同様にまずはNA=2×1016cm-3としたときにWdmax=220nm>tSOIとなっていて、FDSOI構造となっていることがわかるね。つまりWdmaxは今回の計算に考慮しなくて済むね。
Coxは以下のようにバルクMOSと同様。
ここで、従来のCdmがFDSOIだとどう考えればいいかな？
FDSOIのチャネル以下に見える容量をCdm’とでもしておくと、以下のようにCSOIとCBOXの直列容量になることがわかるかな？
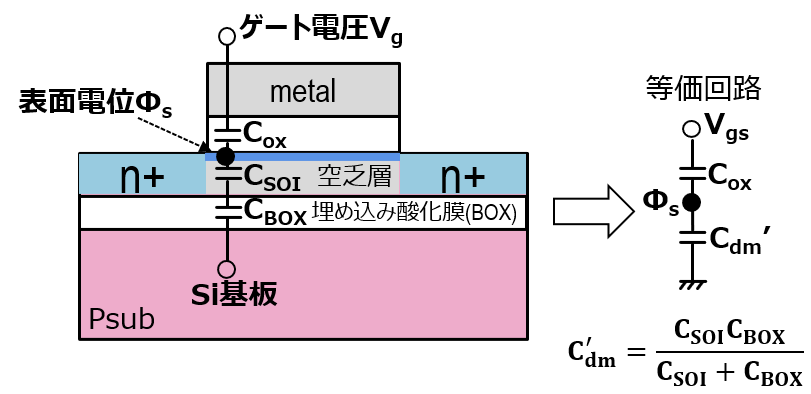
なのでSSを計算するにはCSOIとCBOXを各々計算すればいいってことだね。
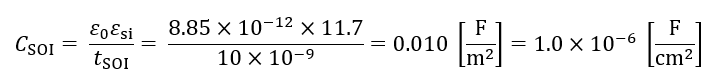
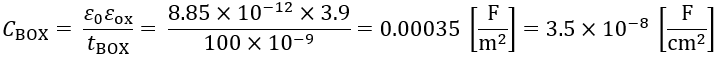
以上からSSを計算すると、
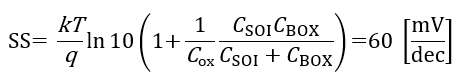
とバルクMOSとほぼ同じ値になったね。
次にNA=2×1018cm-3にすると、これもWdmax=25nm>tSOIなので、FDSOI構造になるね。
あれ？ここで新たに計算するものってなんだっけ？
FDSOIの時点でWdmaxは考えなくていいってことはNAに依存しないってことだから、パラメータの更新はないんだね。つまり以下のようにSSは全く変わらない。
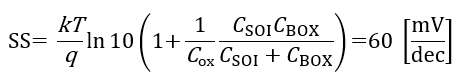
SSの推移もNAに依存せず以下のようになるよ。
これはFDSOI構造の間はこうであって、さらにNAを上げるとtSOI>WdmaxでFDSOIでなくなってしまい、Sファクタの悪化が見えてしまうよ。もちろんNAを上げすぎると上記で挙げたようなデメリットが多いので、FDSOIとしてはSファクタを下げずにある程度NAを上げて短チャネル効果を抑えられることが強みといえるね。
更なる微細化に向けて
今回は微細化に伴うデバイスの進化としてFDSOIを紹介したけど、近年はさらに進化していてFinFETとかGAA(Gate all around)、CFETといったものが出てきているよ。良ければ調べてみてね。今後はチップを縦に積層していくことで集積化を図っていこうとしているみたいだけど、放熱とか課題は多いみたい。
(所感だよ。CFETってのはPMOSとNMOSを縦方向に積んでるんだけど、2023のIEDM(半導体デバイスの最高権威の学会)でもCFETの覇権争いが目立っていたような。いろんな特性面での理由から、PMOSの上にNMOSを積むのがどの発表も共通してて、これがCFETのスタンダードになりそう。来年はもっと競争も激しくなって色んな事実も分かってくるんじゃないかな。
さわざわはプロセスは素人だけど、こういったデバイス構造の進化ってのは、半導体の進化の源を捉えて追っているようでやっぱりワクワクするよね。とても楽しみ。)
ちなみにこれは有名な話だけど、例えば180nmプロセスとかだったら最小チャネル長が22nmという意味であったけど、近年の新デバイス構造を用いた超微細プロセスでは、実際にその長さの値がどこにも存在しないんだって。3nmプロセスだった場合、3nmのチャネル長になっているわけではなく、もはや集積度を表す言葉に過ぎないみたい(詳しくは知らないけど特性はもちろん3nm相当なんだと思う)。
今日はここまで、ほな。
雑談枠
山わさびの納豆に絶賛ハマり中。第3次納豆ブームの到来。納豆ってほんと安いし庶民の味方って思う。納豆ご飯を食べて激動の時代を生き残ることにするわ。
Xアカウント
https://x.com/swzw6112
–お問い合わせ–
以下よりお願いします。
