どうも、さわざわです。
今回はソース接地回路の伝達関数を小信号等価回路から計算しようという内容で、前回の続きになりまっす。前回は小信号等価回路の考え方を覚えることを目的に、nchを例に伝達関数出してみてるので、良かったら先に見てみてねい。
→ソース接地回路について_小信号等価回路を理解しよう編
この記事を読んだらソース接地回路の小信号等価回路からの伝達関数の計算と、周波数特性についてわかります。んじゃあ、さっそく続きからだね。
ソース接地回路の小信号等価回路
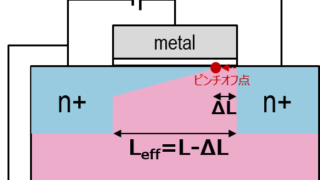
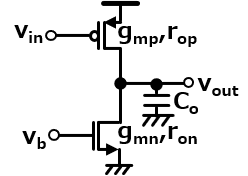
今回扱うソース接地回路は以下のpchダイオードを負荷デバイスにしたものだよ。
彼らを小信号等価回路に変えてみよう。nchの部分は前回と同じで以下のようになってるね。
pchのソースはvddについてるけどこれはac的には0Vなので、小信号等価回路ではgndを等価で良くて、nchのソースとつながるように表せる(voutを軸にパタッと折りたたんで表せるイメージ)。Pchのソースは0Vとして、vgsにはいくらかかってるだろう？
そうだね、だからpchのgmをgmpとするとids=gmpvoutだね。同じくvdsにもvoutがかかってるから、pchのroをropとするとids=vout/ropってなるね。んでこれら電流は全て独立に流れるって考える。nchのgmをgmn、roをronとしとくと、小信号等価回路は以下の右のようにかけるね。
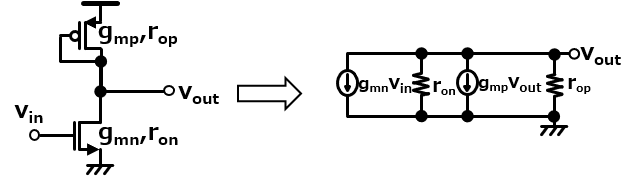
ソース接地回路の伝達関数の計算
前回と同じようにこれでキルヒホッフの電流則から伝達関数を計算してみよう。gmn以外はvoutがかかって電流となっているため、以下のように全てvoutでくくることができるよ。
この際1/roとgmpはコンダクタンス表記しているため(抵抗(インピーダンス)の逆数表記)足し算で表してるけど、直感的に理解するためにインピーダンスで表記するとronと1/gmpとropが並列に入っていて、その並列抵抗にvoutがかかっているということになるね。
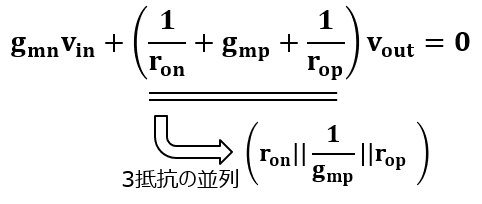
ここで入力デバイスや負荷デバイスが十分長チャネルで、飽和動作させた際にronやropが大きいとすると(固有利得gmroが10~100の場合、インピーダンスとしてronが1/gmより10~100倍大きいということ)、並列抵抗で3つのうち一つだけ抵抗が小さいパスがあることになるので、この際以下のように電流は他の抵抗に流れようとせず1/gmpだけ流れるように近似できることがわかるかな？
よってこの並列抵抗はほぼ1/gmpしか見えていないことになる。そうなると先ほどのキルヒホッフの電流則がかなり簡素化できるね。伝達関数は以下のように表せてこの回路のdcゲインは-gmn/gmpとなるよ。
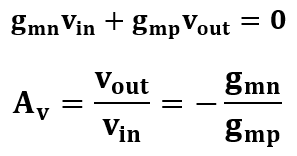
この回路のdcゲインは分母にも分子にも相互コンダクタンスがいるから、一般的にgmによる電圧-電流変換は非線形になるけど、出力で電圧に戻す際に負荷デバイスに1/gmpが見えることで、非線形同士で打ち消して線形性を保てることが特徴だよ。ただ2つのデバイスには同じ電流が流れるため、ゲインを得ようとするには入力デバイスと負荷デバイスのアスペクト比(チャネル長とチャネル幅の比)を変えるほかなく、アンバランスな回路となって寄生容量とかがついたりとデメリットもあったりするね。
ソース接地回路の周波数特性
んじゃあ次は出力に容量がついていたとして、周波数特性がどうなるかを見てみよう。こいつの小信号等価回路はどうなるかな。
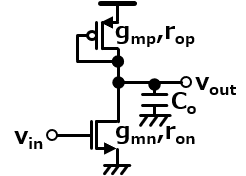
もう出力の抵抗には1/gmpしか見えないことがわかってるので、そこに並列にCoが加わった形になるね。キルヒホッフの電流則から伝達関数を出すと以下のようになったよ。
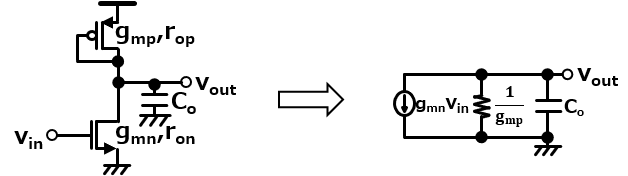
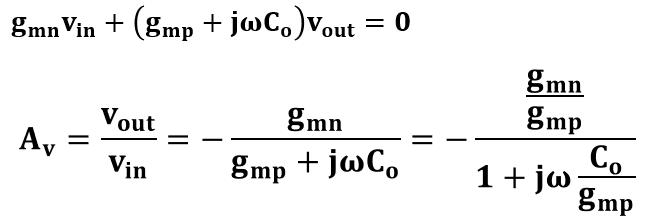
なにやらローパスフィルタ(LPF)のときと似たような形になってるね。LPFと同様に周波数特性を出すとどうなるかな。考え方は以前のLPFの応用に過ぎないので以前の内容を参考にして考えてみてねん。
→ローパスフィルタについて
伝達関数の分母の場合分けと、伝達関数全体での場合分けは以下のようになったよ。LPFと比べて、カットオフ周波数より低周波領域ではdcゲインがかかっていて、カットオフ周波数から高周波数にいくにつれてLPFと同様に-20dB/decでゲインが減衰されていくことがわかるね。
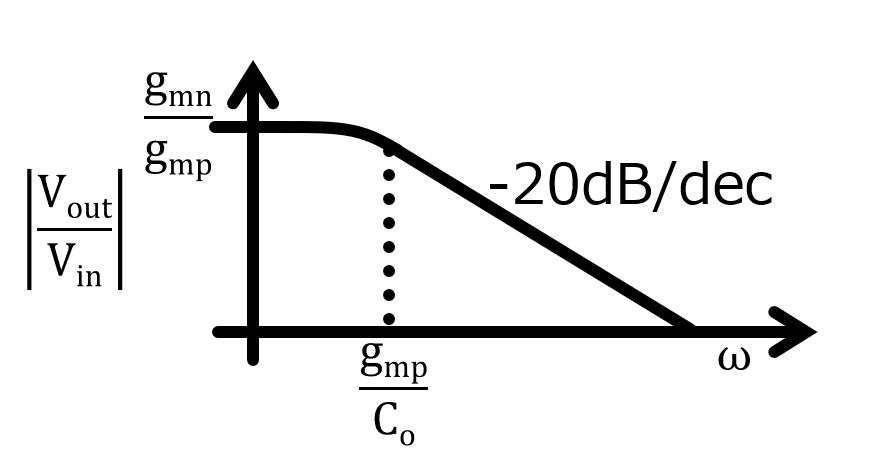
ここでわかるのは、今回のソース接地回路のようなアンプも、LPFにdcゲインをかけたようなものにみてokということで、今回の式でいうと分子の部分にdcゲインが来てることがわかるね。また今回カットオフ周波数はgmp/Coだけど、この1/gmpはこの回路の出力抵抗が来ていることになるよ。
あと容量は出力容量で、その積からカットオフ周波数が算出されてるってことだね。ちなみに今回の出力抵抗はronと1/gmpとropの並列抵抗だったけど、長チャネルなので近似して1/gmpになってるってことだね。
だから最終的に、今回のソース接地回路は以下のような等価回路で表せるね。容量成分が出力容量が支配的で近似できる場合、このAvとRoutが回路によって変わるだけなので考えやすいね。
次回予告
最後に次回予告。
最終的にオペアンプに持っていきたいので、その助走として以下二つの伝達関数と周波数特性も同様に考えてみてほしい。これらは全部ソース接地回路といわれるものだけど、いろんな種類があるんだね。でも特性は違っても考え方は同じだよ。
→ソース接地回路について_いろいろなソース接地回路に触れよう編
雑談枠
昔はちょっとした移動もチャリに乗ってたりしたが、最近は歩くのが楽しく健康意識も高いのか、チャリに乗ることがガクッと減った。乗らなさすぎて、鍵をナンバー式にしてるが頭の中では番号が思い出せない。でも手は覚えていて解除できる。不思議。でもいつか忘れる。
おすすめ書籍紹介(Amazonに飛びます)
Design Of Analog Cmos Integrated Circuit , 2Nd Edition
(↑の原版のIndian版(英語)で2ndからは訳書にない新内容有り、ペーパーバックは安め。英語に抵抗ない方はこっち買うほうが内容的にも値段的にもお得)
Analog Integrated Circuit Design
(網羅的かつ設計観点で深めに学べる印象なのにわかりやすく書いてて初級向け、演習も易しめで取っつきやすい。ただハードカバーのため高い、、)
CMOSアナログ回路入門: LSI設計者のための (半導体シリーズ)
(初学者向け。実用的な内容もあるがあまり深ぼらないので、あくまで勉強するきっかけを作る本な気が。)
Xアカウント
https://x.com/swzw6112
–お問い合わせ–
以下よりお願いします。
