どうも、さわざわです。
今回はノイズが無相関であることの意味について触れていこうと思うよ。ノイズ電流密度とかの計算って以前に記事にしたことがあると思うけど、この時にノイズって普通の電流の計算とかと違うなって疑問に思ったことがない?さわざわは結構疑問に思ってたんだけど、これについて今回は考えてみたので、ノイズの考え方って意味でみんなも勉強していってねい。
この記事を読めば、ノイズ計算の考え方について無相関や有相関が指すことの意味について理解できます。
ノイズの計算のなぜなぜ
いきなりだけど以下の回路図において、dc的な電流I1とI2が決まっていたとして、I3がいくつになるだろう?
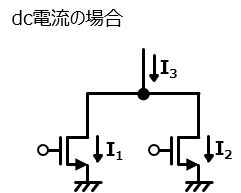
これは非常に簡単で、以下のように和で出せるわけだね。
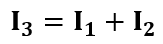
では次に、それぞれのnchはノイズ電流がIn1とIn2と発生していたとして、In3はいくらになるだろう?
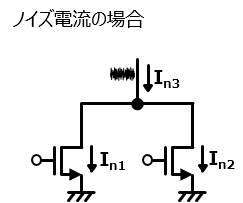
すでにノイズについて勉強してる人からしたら引っかからないかもだけど、これは以下のようにそれぞれを2乗で加算してから√を取るような形になるんだね。
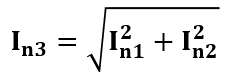
これってなんでだろう?これを今日は考えていこう。
ちなみにノイズについては以下の以前の記事を覗いてみてね!
→ノイズの基礎について
ソースデジェネレーションを用いた電流源とノイズについて
無相関ってどういうこと?
無相関の説明ってのはRazaviのアナログ本とかを読めばよくわかると思うんだけど、ノイズってのは以下のように時々刻々と揺らいでいて、時間によってはプラスなりマイナスなり振れているんだったね。
例えばノイズが以下のように複数あったとして、それぞれが全く独立に揺れていたとすると、ある時点だけピックしても必ずしも二つともプラスに触れているわけではないわけだよね。むしろ反対の方向に揺れていることだってあるはず。
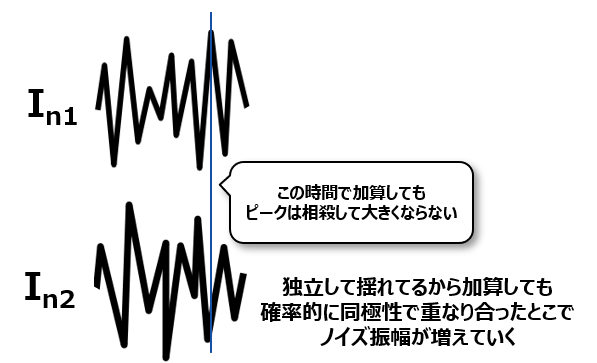
なので↑の時点では二つの加算されてもそんなに増えているようには見えなくて、全部の時間を見てそれぞれ足していくと統計的にノイズの幅自体が増えていくってイメージになるんだ。
上記のように同じ揺らぎ方をしないノイズってのを無相関のノイズって呼ぶんだ。ポイントとしては、確率的にプラスに揺れたりマイナスに揺れたりすることから、単純に加算した表記ができないってことになるよ。
ここで、ある時点でのノイズの加算は必ずしも同じ方向(同じ極性)に向いているわけではないことから、ベクトル表記を用いて次項から考えてみよう。
ベクトルで考えた無相関のノイズの和
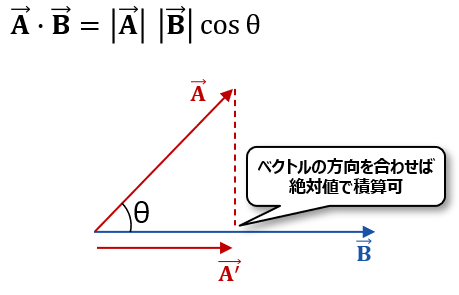
前項から、ここで以下のように最初のノイズ電流をベクトル表記で考えよう。

ただここで求めたいのは電流の大きさであることから、ベクトルを絶対値表記で表したいよ。その場合に加算って以下のようになるよね(さわざわも高校数学とかだいぶ忘れてきちゃってるけど、、)。
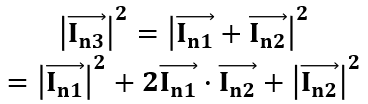
ここで真ん中だけ絶対値表記できていないので、ベクトルの計算をしなくちゃいけなかったよね。
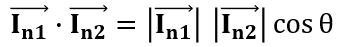
この真ん中の項は↑のようにかけて、これって何を言ってるかというと別方向に向いているベクトル表記の片方をcosθを用いてもう片方と同じ方向に向けて、ようやく絶対値として同じ成分をかけられるって意味だと捉えられるね。
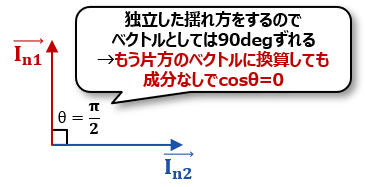
ここでノイズの話に戻ると、さっきのIn1とIn2がばらばらにノイズの揺れ方をしていたので、片方のノイズの中には、もう片方のノイズの成分って全くないわけだね(ランダムに揺れてるのである時点で確率的に増えたり減ったりするだけ)。
なのでここでベクトル表記で考えたときに、以下のようになることがわかるかな?片方のノイズが、もう片方のノイズには影響しないので、θ=π/2。
つまりはcosθ=0となって真ん中の項は消えて、最終的にノイズの加算は以下のようになるんだね。これが無相関のノイズを加算した際に、2乗してから足して√を取るってことにつながるんだね。
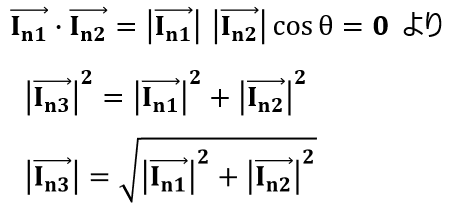
ちなみに有相関とは
有相関なノイズってのは以下のように、同じ揺らぎ方をするノイズのことをいうんだ。
なので例えばある時点でノイズ1がプラスにピークのようなものを持っていた場合に、有相関であるノイズ2もその時点でプラスのピークを持っていて、加算するとそのままプラスにピークが大きくなっていくようになるんだね。
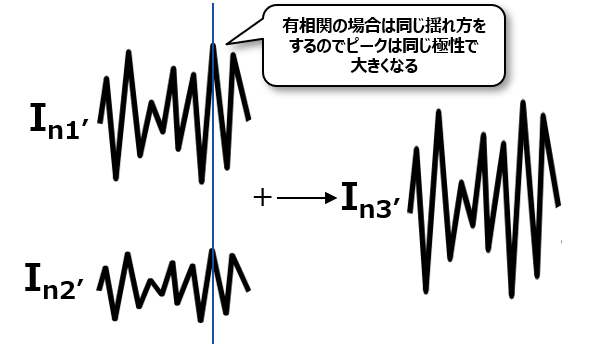
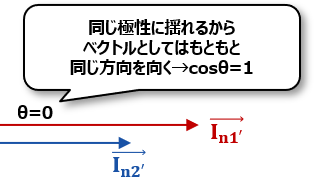
これは加算する際にそれぞれの値が必ず同じ極性を持つことが決まっていることから、ベクトル表記的には以下のようになって、θ=0となるんだ。なので加算は以下のように、見慣れた足し算のように計算していいってことになるんだね。
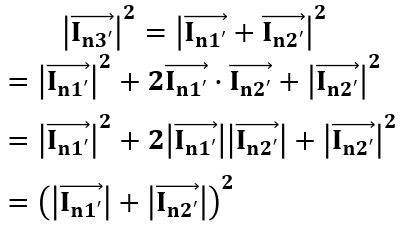

ノイズだけじゃなくて最初のdc電流の加算についても、必ずプラス側に加算されることから有相関な信号っていえて、ちゃんとベクトルを意識して計算した結果この記事の最初のような結果となってるって考えられるよね。

今回の内容から以下で演習積んで理解を深めてみてねん。多分無相関の内容はこの記事のほうが丁寧かもだけど、それをもっての演習が充実してるので。

無相関なノイズと有相関なノイズの一例
無相関なノイズってのは非常に多い。
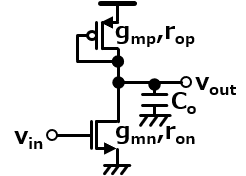
例えば以下のソース接地回路ってのは熱ノイズだけで考えても抵抗とnchとpchがそれぞれノイズ源になるわけで、基本的に別のノイズ源ってのは各々ランダムに揺れるってことになるから、出力部で加算する際に無相関なノイズになるよ。

有相関なノイズは意外とニッチなところで現れたりもするけど、例えば電源ってのもランダムに揺れてノイズ源になるわけであって、これを多くのブロックで共有するわけだから、IRドロップの違いによって振幅は異なるものの、ノイズの揺らぎ方は同じで有相関なノイズっていえるかな。

今日はここまで、ほな。
雑談枠
最近ライオンちゃんが出てないからもっと出してって意見が多い。まあ1個もそんな意見ないけど。
本当にありがたいことに以下の問い合わせフォームからコメントなり質問なりを頂けることが増えてきて、できるだけ休日に一人一人に返信させてもらってるんだけど、メールアドレスが入力されてなかったり有効なものでなかったりで返信できないことがちょくちょくある。。その際は返信できないことはご承知おきください!
おすすめ書籍紹介(Amazonに飛びます)

アナログCMOS集積回路の設計 (基礎編)
(最近第2版が出て原版のupdateが反映された感じ)

アナログCMOS集積回路の設計 (応用編)
(最近第2版が出て原版のupdateが反映された感じ、以下のソフトカバーと比較すると高い気が。。)

Design Of Analog Cmos Integrated Circuit , 2Nd Edition
(↑の原版のIndian版(英語)で2ndからは訳書にない新内容有り、ペーパーバックは安め。英語に抵抗ない方はこっち買うほうが内容的にも値段的にもお得)

Analog Integrated Circuit Design
(網羅的かつ設計観点で深めに学べる印象なのにわかりやすく書いてて初級向け、演習も易しめで取っつきやすい。ただハードカバーのため高い、、)

CMOSアナログ回路入門: LSI設計者のための (半導体シリーズ)
(初学者向け。実用的な内容もあるがあまり深ぼらないので、あくまで勉強するきっかけを作る本な気が。)
Xアカウント
https://x.com/swzw6112
–お問い合わせ–
以下よりお願いします。